品质过程控制与统计分析（一）

产品或者服务的质量始终是企业能够在市场立足的根本，因此，如何保证产品和服务的质量，也是企业内部运营的重中之重。在精益管理的目标中，质量也位列QCD的第一位。

之前我们谈过品质过程控制《品质过程控制》，在生产过程中通过对品质产生影响的点加以识别和检查，保证生产过程处于我们想要的状态，从而保证产品的理想状态。

这样的控制手段能够有效地管控过程变量，但是对于目前的过程情况如何？是处于稳定的良好状态还是已经处于问题边缘？应该如何处理？这些就需要我们运用一些统计的方法，拿出数据来说话了。

首先，我们先来了解一个很重要的图形——正态分布图。正态分布图的形状有点像寺庙的钟，所以也叫钟形曲线，如下图：

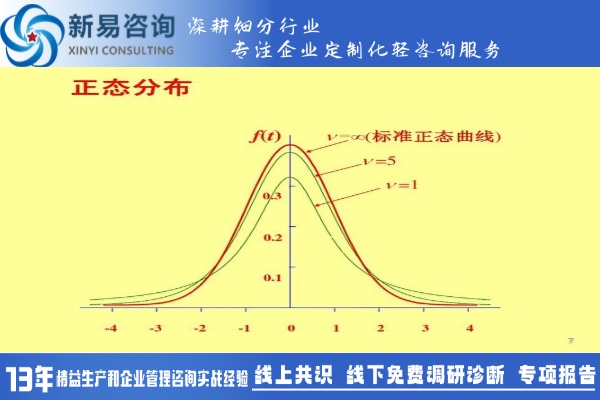
为什么要说这个曲线呢？因为经过分析很多统计数据发现，我们面对的绝大多数参数都符合正态分布，比如说一个国家的人群身高、体重等等，包括我们在生产中面对的各种参数也是如此。

例如我们在某工厂对其配方加入量的波动情况进行统计，得到的图形也是一个中间高、两边低的形状，如下图：

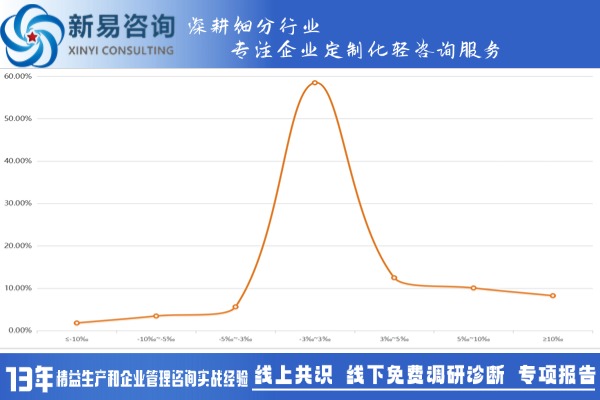
而这种分布的特性，为我们做产品的品质数据统计和分析提供了依据。统计学告诉我们，要描述一个参数的数据情况，至少需要平均值和标准差这两个维度。

对于正态分布来说，同样是使用这两个维度来进行描述。在画出参数的分布图时，我们会首先用到平均值，具体的画法如下：

①连续观察、记录需要分析的参数数据，数据量越大越好，传统的统计学要求数据量不少于20个；当前的大数据时代，有电脑和各种软件的辅助，数据量多多益善。

②计算平均值，将所有的数据相加，除以数据的个数减1，得到这个参数的平均值。

μ=（X1+X2+X3+……+Xn）/（n-1），n为记录数据的个数

③将数据划分为不同的区间段，划分方法在统计学中有明确详细的要求，但在日常工作应用中，我们是以计算的平均值为中心，向两边以固定的距离划分区间，比如每隔5或者10做为一个区间，当然也可以用我们的经验来设定一个合理的区间间距，最终划分的区间段要能够覆盖数据的最大值和最小值。

④计算各区间内数据的数量，跟数据总量对比，得出每个区间内数据占总量的比例，再以区间为横坐标、区间数据比例为纵坐标画出折线图或者直方图《QC七大手法的使用（六）——直方图》，就可以初步得到这个参数的正态分布图了。

画出分布图后，如何进行分析？关注新易咨询，我们将在下一篇文章中继续分享。