品质过程控制与统计分析（二）

在上一篇文章中，笔者给大家介绍了“正态分布图”（点击查看）《品质过程控制与统计分析（一）》。画出我们需要分析的数据分布图后，我们就需要用到前篇文章中提到的另外一个评价参数——标准差了。

在理想状态下，我们希望生产过程中的各个参数都稳定在一个值上，但在现实中，这些参数总是在一个范围内波动的，而标准差就是衡量这种波动大小的参数，通常用希腊字母σ来表示。

σ的数值越大，表示这个参数的波动越大，对应到分布图上，我们画的这个“钟”就越矮越扁；而σ的数值越小，则表示波动越小，对应的“钟”也就越高越窄。

从图形上判断，我们就可以直观地知道参数的波动大小。比如下图中，这个参数的三组不同时间的分布曲线，橙色的波动就小于黄色和蓝色，蓝色曲线是波动最大的。

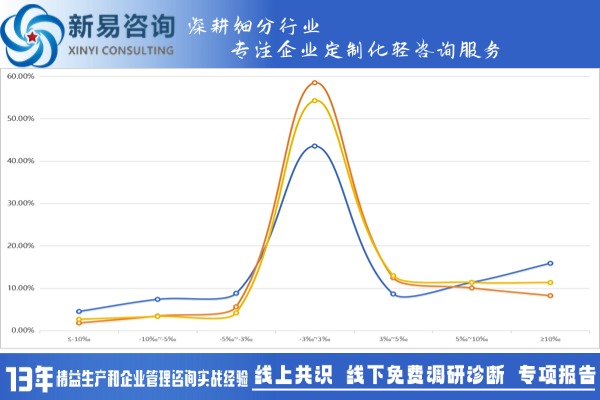
但是这也仅仅是一个纵向的对比，那么有没有一个客观的评价标准呢？有，而且这个评价标准就是σ的水平。可能大家都听说过六西格玛管理，这种管理方法就是从σ的控制水平引申发展起来的。

在正态分布中，“钟形曲线”下与坐标轴之间围成的面积是1（或者100%），代表参数出现的所有可能性都在曲线上，而出现的可能性大小则由曲线的高低决定。

比如上图中，参数出现在-3‰~3‰范围内的可能性就高于出现在其它区间的可能性。而通常我们对某个参数的控制是有一个区间的，也就是有上限和下限。这时候联系分布图我们就知道，越高越窄的“钟”，控制参数落在上下限之间的可能性就越大。

当我们以平均值为中心，向横坐标轴的左右两侧各以一个σ为单位区间做图时，我们就可以用有多少个σ落在了上下限之间来做为参数控制水平的评价标准。

比如在上下限之间有2个σ，那对于平均值的单侧（左侧或者右侧）而言，就只有1个σ，我们称为1σ水平，它对应的钟形曲线下方的面积是68.27%，也就是说在1σ的控制水平下，参数合格的可能性只有68.27%，这意味着对应到产品上，每1万件产品将产生3173件不合格品。

通常我们的工业生产控制水平大约在3个σ左右，它对应的合格率是99.73%。这个数值看起来好像还不错，但对于大规模的生产而言，这意味着每1万件产品将出现27件不合格品。而6σ水平为99.9966%，也就是它的不合格率为3.4ppm（百万分之3.4），每1百万件产品中仅出现3.4件不合格品。

我们知道了如何来计算一组数据的平均值μ、标准差σ，并画出分布图，结合参数控制上下限来判断我们现在的控制水平如何。下面真正要做的就是如何将我们的控制水平从2σ、3σ提高到4个、5个、6个σ了。关注新易咨询，我们将在下一篇文章中继续分享。