QC七大手法的使用（七） ——控制图

上一篇我们介绍了直方图。直方图是对一个特性指标的一个样本数据的分布描述，而当我们将多个样本数据的直方图按一定的顺序（一般是时间顺序）排列起来，就得到了我们今天要讲的QC七大手法的最后一种——控制图。

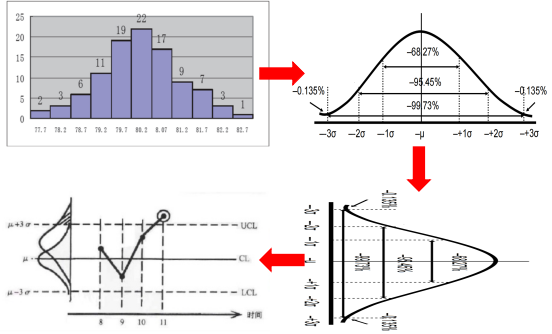
控制图，又叫管制图、SPC控制图、SPC管制图，是对过程质量特性进行测定、记录、评估，从而监察过程是否处于控制状态的一种用统计方法设计的图，由休哈特在20世纪20年代设计发明（PDCA循环也是休哈特提出的）。

控制图分为计量型和计数型两类，计量型控制图，如均值-全距控制图、均值-标准差控制图、单值-移动全距控制图x—Rm等，计数型控制图，如不良率控制图p、不良数控制图np、缺点数控制图c、单位缺点数控制图u等。

典型的控制图如下图：

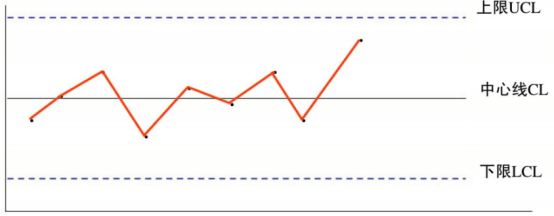
控制图纵轴为产品的质量特性，横轴为时间顺序或产品编号。图中中心线CL、上控制限UCL、下控制限LCL由计算得到。计算方法如下：

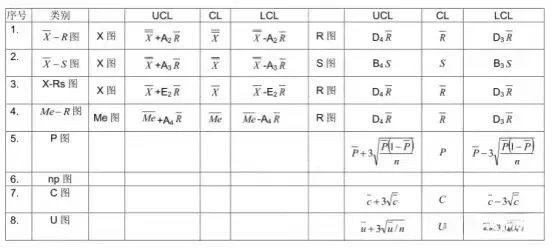
控制图依据统计学原理设计，其原理和过程不在此详述，重点讲解控制图的绘制方法和异常判定。

以最为常见的均值-全距控制图为例。

例：螺栓拧紧工序，对螺栓拧紧扭矩进行动态管理。

扭矩规格为：15.0±5.0kg·cm。

步骤：

①收集数据，每天随机5个，连续收集20天

②计算每天5个产品数据的平均值

③计算每天5个产品数据的全距R

④计算20天平均值的平均值

⑤计算20天全距R的平均值；如下表：

⑥查看“管理界限计算系数表”，每天样本大小n=5时，A2=0.579，D3无取值，D4=2.115；

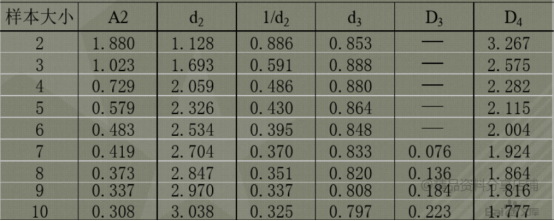
⑦计算

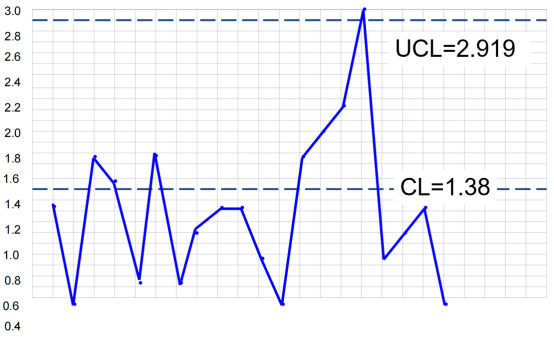
CLR==1.38，

UCLR=D4=2.115×1.38=2.919，

LCLR不做计算,

CL==16.316

UCL=+A2=16.316+0.579×1.38=17.115

LCL=-A2=16.316-0.579×1.38=15.517

另外，也可以用3σ计算UCL、LCL取值，即：

UCL=CL+3σ，

LCL=CL-3σ，

这是因为在正态分布中，数据落在3σ区间内的概率为99.73%，或者说数据不在正常范围内的概率只有0.27%，根据统计学原理，

小概率事件在单次测量中被认为是不可能事件，所以可以用CL±3σ来做为上下控制限。

⑧绘制R图

⑨绘制图

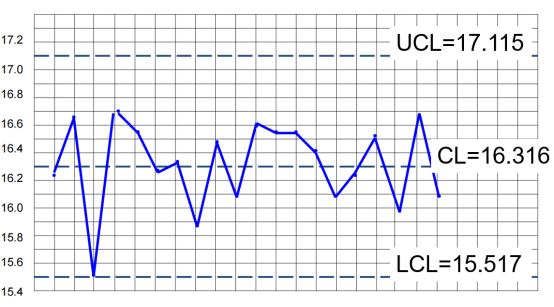
到这里，我们完成了控制图的绘制。

但是，我们绘制控制图，是为了对质量特性进行评估、分析、监控，因此，我们还要通过控制图来分析数据是否出现了异常状态。

控制图的异常判断准则有以下几条：

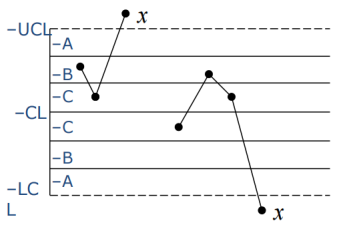
1、一个数据点落在A区以外

可能原因：原材料不合格，设备故障，测量错误等。

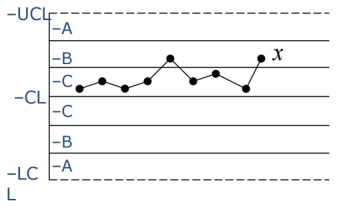
2、连续9点落在中心线同一侧

可能原因：中心值发生偏移。

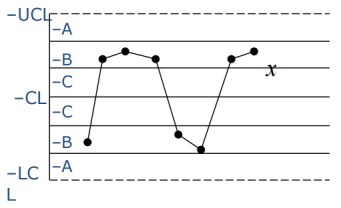
3、连续6点递增或递减

可能原因：工具逐渐磨损，操作者疲劳或者技能变熟练，工作环境改变。

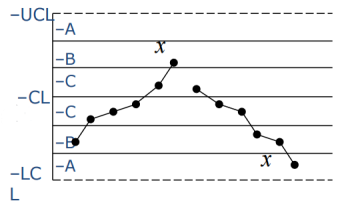
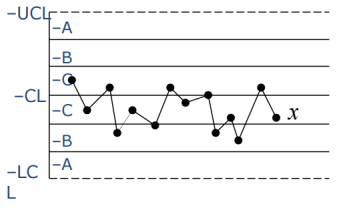
4、连续14点相邻点总是上下交替

可能原因：两台设备或者两位操作者交替引起的系统效应，数据分层不足。

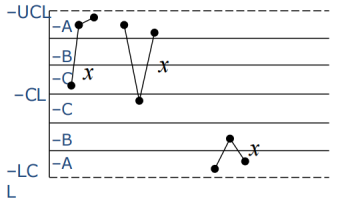
5、连续3点中有2点落在中心线

同一侧B区以外

可能原因：过程控制过严，材料有差异，检验方法有区别。

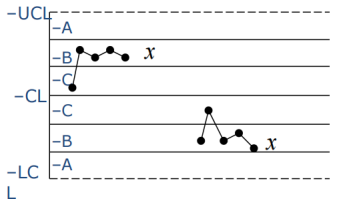
6、连续5点中有4点落在中心线

同一侧C区以外

可能原因：过程控制过严，材料有差异，检验方法有区别。

7、连续15点落在C区之内

可能原因：制程经过改善，变异数降低，或者数据分层不够，数据虚假。

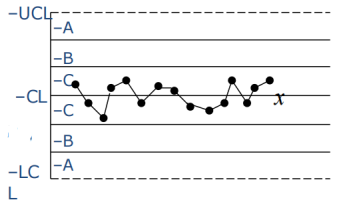
8、连续8点落在中心线两侧

且无1点在C区中

可能原因：数据来自两个群体，分层不够。

根据这些异常判断准则，我们就可以根据控制图快速判断是否发生了异常，并对异常可能的原因有一个初步的判断。

当然，我们以上绘制的控制图，是分析用控制图，主要是用来对质量特性进行分析的。

除此之外，还有控制用控制图，在生产过程监控中起着重要的质量控制作用。

一般来说，当过程处于稳定状态时，只需将绘制出的分析用控制图的CL、UCL、LCL延长，即可在图上将生产过程的实时数据绘制在图上，作为控制用控制图，进行过程质量监控。

控制图相较QC七大手法中的其他六种，使用门槛更高，过程也更为复杂，但对于过程的监控，有着其他手法不具备的优势。

七大手法各有其侧重，要根据实际情况，灵活选用合适的方法加以运用，才能有效地解决生产中的问题。

☞点击文字查看《4+1组织赋能系列课程》☜